7.2. Sortowanie tablicy. Pomiar średniej złożoności obliczeniowej
Nazwa programu: czas.pas
Wariant 1: generacja ciągu liczb w tablicy
jednowymiarowej, sprawdzenie poprawności sortowania
P1. Dlaczego tablica a została skopiowana
do tablicy b?
Wariant 2: pomiar średniej złożoności obliczeniowej
Przedstawiamy łatwą metodę pomiaru złożoności czasowej
wykonania dowolnego algorytmu. Rozważana operacja musi być powtórzona
wybraną liczbę razy (np. rep = 10000), tak aby można było
zmierzyć czas jej wykonania. Należy przy tym rozważyć, czy badana
operacja może być powtarzana samodzielnie, tak jak to jest w przypadku
generacji ciągu liczb w tablicy. Zauważmy, że powtarzanie operacji
sortowania ciągu liczb nie może być wykonane dla jednokrotnie wygenerowanego
ciągu, ponieważ czas sortowania już posortowanej tablicy nie może być
uważany za przypadek ogólny. Tak więc, aby wyznaczyć złożoność sortowania,
należy wykonać następujące czynności:
- zmierzyć τgs – czas wykonania
rep powtórzeń dwóch operacji, czyli generacji ciągu
n liczb losowych w tablicy oraz sortowania (łącznie),
- zmierzyć τg – czas wykonania
rep powtórzeń samej generacji,
- obliczyć τs = τgs
– τg, czyli czas samego sortowania w zależności
od n.
Zwykle wykonuje się rysunek przedstawiający wyniki
pomiarów i obliczeń w zależności od n, czyli rozmiaru
zadania. Punkty na tym rysunku mają rzędne o wartościach losowych.
Jeśli chcemy aproksymować je za pomocą wybranej funkcji, czyli
np. znaleźć współczynniki paraboli, której wykres przebiegałby dostatecznie
blisko tego zbioru punktów, to powinniśmy zastosować odpowiedni algorytm
(por. [1]).
Jeżeli jednak tak dokładna analiza nie jest potrzebna,
to znając oszacowanie najgorszego przypadku wykonania badanej
operacji (np. dla sortowania ciągu w tablicy metodą prostego wybierania
jest to O(n2)), możemy obliczyć wartości
r(n) = τs(n)/(τs(n/2))
w zależności od n. Tak więc r(n) określa,
jak rośnie czas potrzebny na wykonanie operacji po dwukrotnym wzroście
rozmiaru zadania. Jeśli wartości r(n) dążą do 4 wraz
ze wzrostem n, to złożoność czasowa tej operacji jest rzędu
n2; jeśli dążą do 8, to złożoność jest rzędu n3
itd.
Dobrze jest wykonać jeszcze jeden rysunek, zawierający
wykres r(n), zachowując taką samą podziałkę dla
wartości n jak na poprzednim rysunku. Punktów tego wykresu
nie należy łączyć żadną linią. Jeśli chcemy mieć więcej punktów,
to wykonujemy pomiary dla pośrednich wartości n.
Jako przykład w tabeli 7.1 oraz na rysunkach 7.1
i 7.2 podano wyniki badania algorytmu sortowania ciągu liczb
w tablicy metodą prostego wybierania.
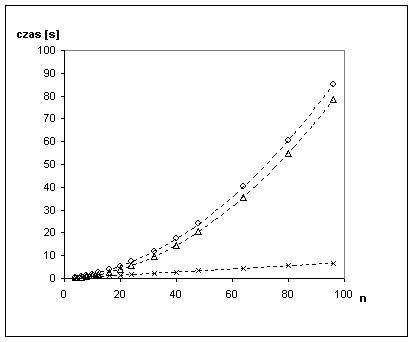Rys. 7.1. Wykres czasu wykonywania operacji w zależności
od rozmiaru zadania (n): o - generacja i sortowanie, x - generacja,
Δ - sortowanie
Tabela 7.1. Wyniki pomiaru: τgs,
τg oraz obliczenia τs i r
w zależności od n (czas w sekundach, rep = 10 000, komputer
z procesorem 486DX (DLC) 33 MHz)
| n |
τgs |
τg |
τs |
τs(n)/(τs(n/2)) |
| 4 |
0.60 |
0.33 |
0.27 |
- |
| 6 |
0.99 |
0.44 |
0.55 |
- |
| 8 |
1.38 |
0.60 |
0.78 |
2.89 |
| 10 |
1.92 |
0.77 |
1.15 |
- |
| 12 |
2.42 |
0.88 |
1.54 |
2.80 |
| 16 |
3.79 |
1.15 |
2.64 |
3.38 |
| 20 |
5.43 |
1.43 |
4.00 |
3.48 |
| 24 |
7.31 |
1.70 |
5.61 |
3.64 |
| 32 |
11.81 |
2.25 |
9.56 |
3.62 |
| 40 |
17.36 |
2.80 |
14.56 |
3.64 |
| 48 |
23.95 |
3.35 |
20.60 |
3.67 |
| 64 |
40.20 |
4.50 |
35.70 |
3.73 |
| 80 |
60.64 |
5.61 |
55.03 |
3.78 |
| 96 |
85.13 |
6.70 |
78.43 |
3.81 |
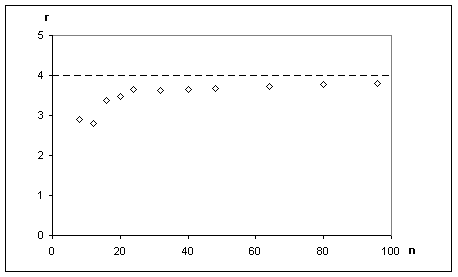Rys. 7.2. Wykres r(n) = τs(n)/(τs(n/2))
do oceny rzędu średniej złożoności czasowej operacji sortowania ciągu liczb
w tablicy metodą prostego wybierania
P2. Wykonać pomiar średniego czasu sortowania
zadanej liczby ciągów losowych o długości n = 5, 10, 15,...,
50, 60, 70, 80, 90, 100. Wykonać dwa rysunki: na pierwszym umieścić
trzy wykresy: τgs(n), τg(n)
oraz τs(n), a na drugim obliczone wartości
r(n) = τs(n)/(τs(n/2))
w zależności od n.
P3. Zaprojektować algorytm zbierania informacji
niezbędnych do oceny średniej złożoności czasowej.
[1] Balińska K., Zwierzyński
K. T., Projektowanie algorytmów grafowych, Wyd. PP, 2002.